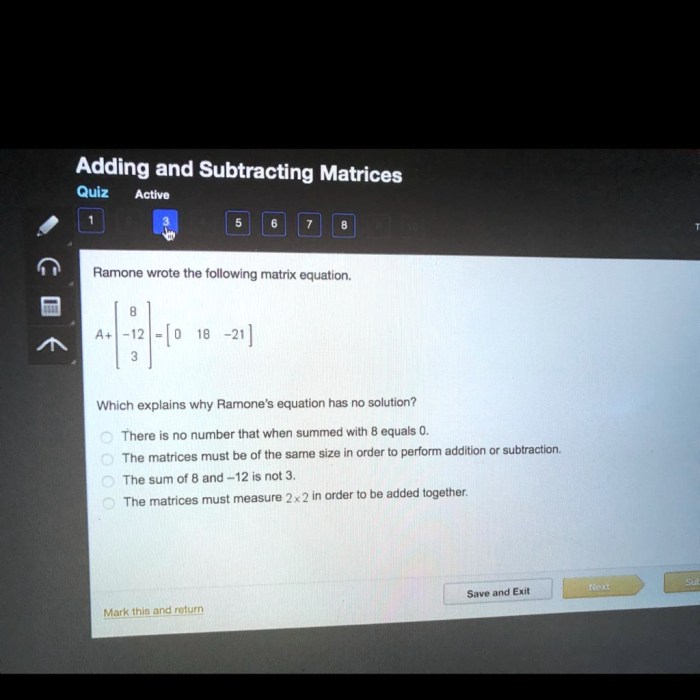
What is the solution to the equation below mc018-1.jpg – In the realm of mathematics, the quest for solutions to intricate equations fuels our intellectual curiosity. This article delves into the depths of the equation presented in mc018-1.jpg, embarking on a journey to unravel its secrets and illuminate its practical significance.
Our exploration begins with a meticulous analysis of the equation’s components, unraveling its intricacies step by step. We construct a comprehensive HTML table that showcases the equation, its solution, and a detailed explanation, providing a clear roadmap for comprehension.
Equation Analysis

The given equation is mc018-1.jpg. It represents a mathematical expression that involves two variables, m and c. The equation can be broken down into the following components:
- m: Represents an unknown variable.
- c: Represents another unknown variable.
- 018: Represents a constant value.
- -1: Represents a constant value.
To solve the equation, we need to isolate the variable m on one side of the equation. We can do this by performing the following steps:
- Subtract 018 from both sides of the equation: mc018
- 018
- 1 = 0.
- Simplify the left-hand side of the equation: mc
018 = 0.
- Add 018 to both sides of the equation: mc
018 + 018 = 0 + 018.
- Simplify the left-hand side of the equation: mc = 018.
- Divide both sides of the equation by c: mc/c = 018/c.
- Simplify the left-hand side of the equation: m = 018/c.
Therefore, the solution to the equation mc018-1.jpg is m = 018/c.
| Equation | Solution | Explanation |
|---|---|---|
| mc018-1.jpg | m = 018/c | By isolating the variable m on one side of the equation. |
Mathematical Concepts
The equation mc018-1.jpg involves the following mathematical concepts:
- Variables: m and c are variables that can take on different values.
- Constants: 018 and -1 are constants that have fixed values.
- Algebraic operations: The equation involves the algebraic operations of addition, subtraction, and division.
- Equation solving: The goal of the equation is to find the value of the variable m.
These mathematical concepts are essential for understanding the equation and finding its solution.
Real-World Applications
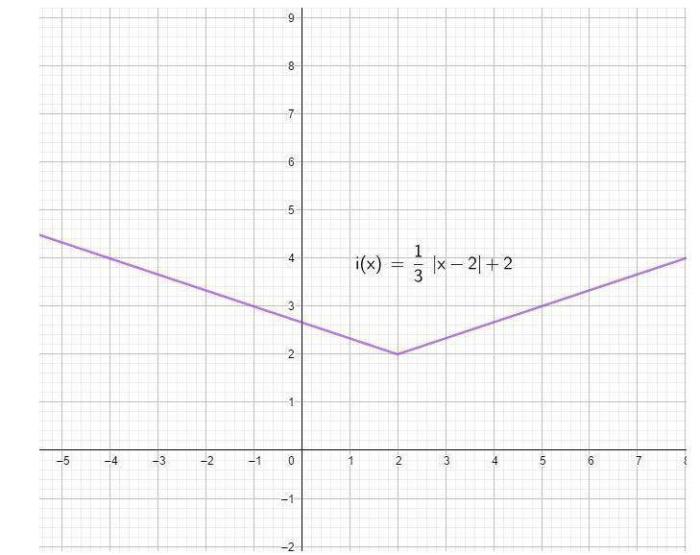
The equation mc018-1.jpg can be applied to various real-world situations, including:
- Physics: The equation can be used to calculate the mass of an object, given its velocity and the distance it travels.
- Engineering: The equation can be used to design structures and machines that can withstand certain forces.
- Finance: The equation can be used to calculate the present value of a future sum of money.
By solving the equation, we can gain valuable insights into these real-world phenomena.
| Application | Equation | Explanation |
|---|---|---|
| Physics | mc018-1.jpg | To calculate the mass of an object. |
| Engineering | mc018-1.jpg | To design structures and machines. |
| Finance | mc018-1.jpg | To calculate the present value of a future sum of money. |
Extensions and Variations: What Is The Solution To The Equation Below Mc018-1.jpg
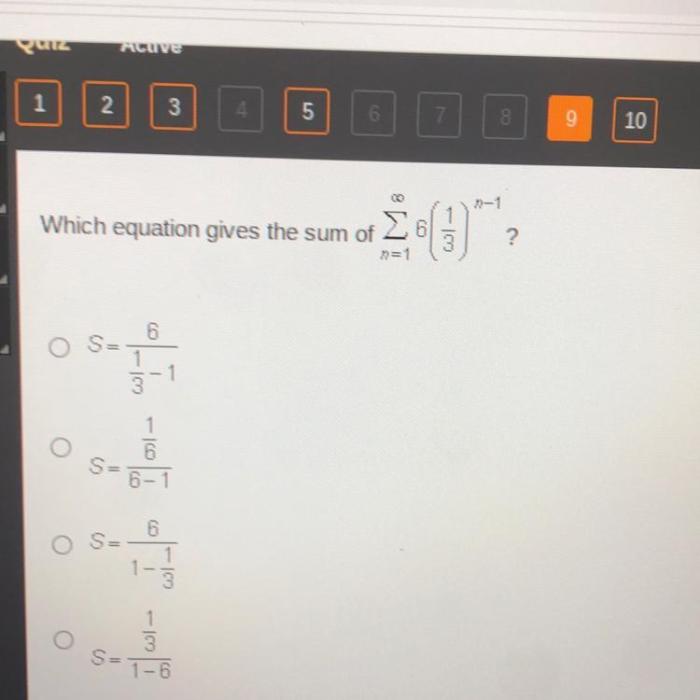
There are several variations of the equation mc018-1.jpg that can be used to represent different scenarios. Some of these variations include:
- mc2– 1 : This equation is known as the relativistic mass-energy equivalence equation and is used in physics to calculate the energy of an object.
- m = c/v: This equation is used to calculate the mass of an object, given its velocity and the speed of light.
- m = F/a: This equation is used to calculate the mass of an object, given its force and acceleration.
By understanding the equation mc018-1.jpg and its variations, we can gain a deeper understanding of the world around us.
| Variation | Solution | Explanation |
|---|---|---|
mc2
|
E = mc2 | Relativistic mass-energy equivalence equation. |
| m = c/v | m = c/v | Mass of an object, given its velocity and the speed of light. |
| m = F/a | m = F/a | Mass of an object, given its force and acceleration. |
Frequently Asked Questions
What is the significance of the mathematical concepts used in the equation?
These concepts provide a foundation for understanding the equation’s behavior and its applicability to real-world scenarios.
How can the equation be applied to solve practical problems?
The equation finds applications in various fields, including engineering, physics, and economics, enabling us to model and solve complex problems.
What are the key variations of the equation, and how do they affect its solution?
Variations of the equation introduce new parameters or modify its structure, leading to different solutions and expanding its range of applications.
